Colour rendering in binoculars and lenses
1. Colours and transmission
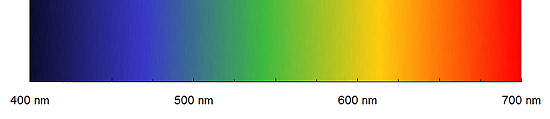
Before we pass to details a word or two as an introduction. The visible light, perceived by the human eye, is in fact electromagnetic radiation with wavelengths ranging from 390 to 750 nm (some people are able to respond to a bit wider spectrum e.g. from 380 to 780 nm).
Please Support UsIf you enjoy our reviews and articles, and you want us to continue our work please, support our website by donating through PayPal. The funds are going to be used for paying our editorial team, renting servers, and equipping our testing studio; only that way we will be able to continue providing you interesting content for free. |
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
The range of the radiation with energies higher than the visible spectrum (the left side of the picture shown above), which stretches from 400 to 10 nm we call ultraviolet. The waves with the lengths longer than 700-750 nm we call infrared.
What’s interesting, good optical glass in itself is very achromatic – it means it lets through in the visible spectrum the same wavelength in the same way. You can confirm that looking at the graph below.
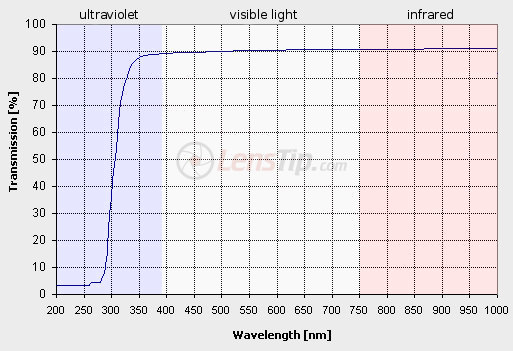
It is the transmission curve of light which passes through a flat glass plate. As you see from the border between ultraviolet and visible light to the border between visible light and infrared about 90% of light is transmitted. The graph is so flat that there are no light colours visible. The problem is of a different nature. The glass plate has two air-to glass surfaces. The graph above shows very clearly that on one such a border only 95% of light passes through and 5% is reflected. Apparently the loss is not much but we are discussing now just one optical element. Typically, optical instruments, constructed nowadays, consist of from several to more than a dozen glass elements and in such a case the reflection of light from air-to-glass surfaces becomes a serious problem. How serious, though? Actually you can count it easily.
A simple set of binoculars or a simple lens means about ten air-to-glass surfaces. For example in typical and produced for several dozen years Porro binoculars we deal with exactly ten surfaces (an achromatic lens has two surfaces, divided Porro prisms have four surfaces, the Kellner achromatic eyepiece (or RKE) has four surfaces as well). Taking into account the fact that on one air-to-glass surface you lose about 5% of light you can easily find that only 60% of light entering the objectives will pass through the whole instrument.
It’s not all. Currently the optics is much more complex than it used to be. Zoom lenses with optical stabilization can be composed of over 20 lenses. The most expensive pairs of binoculars can have objective lenses made of 3-4 elements. As a result the number of air-to-glass surfaces can increase to about 15. Such an instrument will let through only 46% of light. One of the most extreme examples is the Canon EF 70-200 MM f/2.8L IS II USM lens which consists of 23 elements positioned in 19 groups. In its case we deal with as many as 38 air-to-glass surfaces! If you left them to their own devices such a lens would deliver to the detector only 14% of the entering light!
During three hundred years of constructing and using optical instruments that problem was left untouched. The solution was discovered kind of accidentally in 1935 in the German Zeiss factories. It turned out that if you coat the glass with a thin layer of certain substances less light is reflected from the surfaces. Very quickly people also understood why.
The refractive index n for typical glass is 1.5-1.8; for air it amounts to 1.0. The refraction on an air-to-glass surface happens exactly because these two indexes (but also the density of a material and the speed of the electromagnetic radiation in a specific material) differ so significantly. The key to the success is covering an air-to-glass surface a thin layer of a substance (so-called antireflection coating) which refractive index is lower than that of glass but higher than that of air. Not very complicated mathematical-physical divagations give us a simple formula for an exact value of that refractive index – it must be a square root of the used glass’s refractive index. Overall, after the coating, the situation seemingly gets complicated. Instead of one air-to-glass surface we get two: first the light meets an obstacle in the form of an air-to-coating surface and then a coating-to-glass surface. The whole charm of such a solution is that on each of these borders the density change is lower so the amount of reflected light decreases to about 1%. To sum up when one air-to-glass surface reflected 5% of light, now two surfaces with a coating reflect not more than 2%. The benefit is very clear to notice.
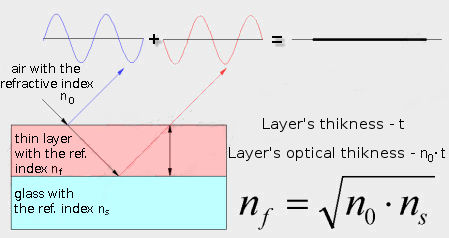
What’s more, not only the kind of a coating is important but also the thickness of the layer. If we choose the right parameters we can make the waves, reflected from the air-to-coating surface and the coating-to-glass surface, damp down each other because there will be an appropriate shift in their phase. It is another characteristic of good anti-reflection coatings – they remove from the optical system the light reflected from the surfaces, increasing the overall image contrast and removing unwanted flares from the optical instrument.
So far we’ve been describing the problem theoretically only. In practice a question can be asked: is it easy to find a substance which would be good as an antireflection coating? The crown glass, the most often used in optics, has the refractive index n = 1.52 which means a perfect material to make an antireflection coating of should have the refractive index of 1.23. The problem is such a solid substance doesn’t exist. The closest equivalent, additionally being rather simple, is the magnesium fluoride (MgF2) with the refractive index amounting to 1.38. Such a value is a bit higher than those demanded 1.23 so magnesium fluoride is the most effective as an antireflection coating of glass with higher refractive index (it works with glass with n = 1.90 the best). Among other factors it is also a reason why transmissions of different optical instruments, even though all their air-to-glass surfaces are coated by the same substance, can differ significantly. The amount of reflected light is influenced not only by the antireflection coating but also the glass itself. An example of cooperation between magnesium fluoride and typical glass is presented on the graph below.
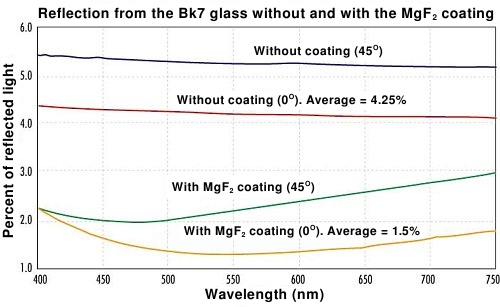 |
This picture shows one important thing. The efficiency of the magnesium fluoride is the highest near 500-600 nm wavelength and drops noticeably at both ends of the spectrum. Seemingly the differences are not high but they relate to one layer only. If there are many coated surfaces, different angles of light, different kinds of glass and also flaws and mistakes during the production process, it can happen the overall transition of the whole instrument for the yellow colour (so in the area around 550-650 nm) will be more than a dozen-several dozen percent higher than for the blue colour (about 400-480 nm). Here we reach the core of the problem which is so keenly felt when it comes to optics produced behind historical already Iron Curtain.
As we don’t want to sound groundless we will present several specific examples. Let’s take one of the most popular Soviet and Russian binoculars so the BPC5 8×30 model, even today available in perfect condition on several Internet auction sites. This pair of binoculars is praised for good build quality, small weight, handiness and decent optics offered at affordable price. It’s enough to look through it, though, to find out the image is quite dark and, most of all, significantly yellowish. Everything becomes clear when you consult the transmission graph of this model.
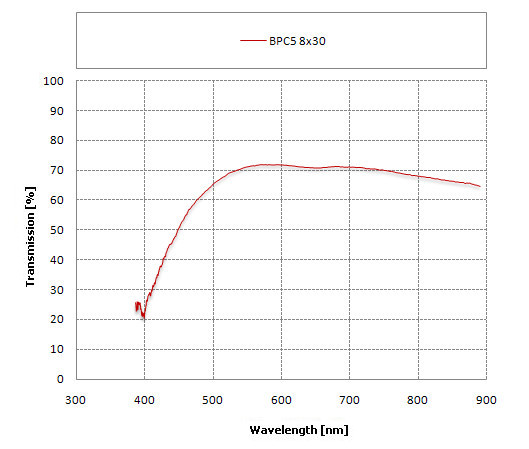 |
The most of light, but not more than 70%, the binoculars let pass through near 600 nm so exactly for yellow light. The transmission of red light is only slightly lower. The problem, however, is situated in the area of the shortest wavelengths. The transmission of purple light reaches just 20-30% and for blue light the result is less than 50%. Several dozen percent of difference between yellow and blue produces exactly that result – damn yellow-coloured image.
The production of binoculars in the former Soviet union had to be fast, cheap and in big quantities; small wonder the quality control was just average (but still far better than nowadays in some Far East factories). It might suggest that even then, several dozen years ago, if the production process, the design of the optics and the coatings had been looked after more diligently, the results could have been better. We didn’t omit to check it. Our next test object is a pair of binoculars which have been produced for a long period of time- from the 70’s of the twentieth century practically up to now – the PZO LP7×45, a Polish army equipment. Since the very beginning it has boasted single layer coatings of magnesium fluoride.
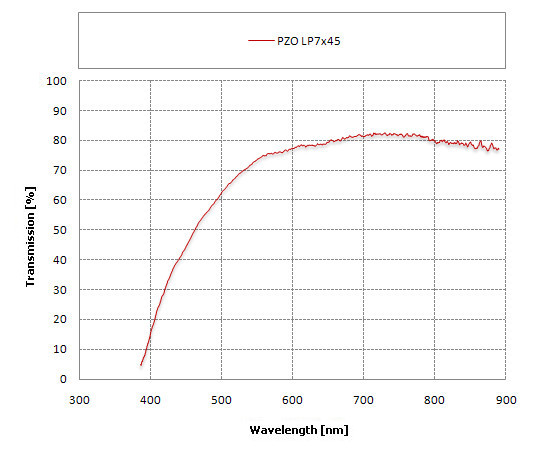 |
The image this set of binoculars gives you is also very yellow – some might think even more so than the image of the BPC. It is because of equally weak performance at the shortest wavelengths as that of the Russian device – the maximum transmission in both cases is situated in fact on the border between the visible light and the infrared. The one saving grace of the PZO is the fact that its overall (average) transmission level is higher than that in the BPC5 8×30.
The Jena products are recognized to be the best optics coming from the former Eastern bloc countries. After 1945 the whole optics, produced there, was covered by blueish one layer coatings Zeiss T, which in 1978 was changed into multilayer coatings with characteristic orange-yellow hue (T3M). For the purposes of our article we decided to test the transmission of a Carl Zeiss Binoctem 7×50 model, produced in 1961 but being in perfect condition. It features the older single layer coatings then.
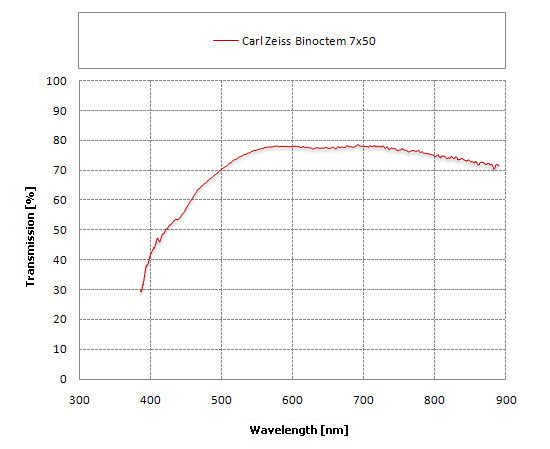 |
We deal here with coatings of the same type as in Russian and Polish optics but the results, as you see, are noticeably better. The transmission doesn’t reach 80% but its graph is more flat; the performance in the blue part, although far from perfect, remains definitely better than in the PBC or the PZO. As a result, although the image provided by the Carl Zeiss Jena binoculars is still yellowish as far as the contemporary standards go, it is better than that of models coming from Russian or Polish factories.
In order to get a good assessment of the situation of single layer coatings we should show how fared a set of binoculars produced by one of the best manufacturers on the market. The Leica company could undoubtedly be counted as such (several dozen years ago that company was called Leitz). We’ve had an opportunity to look closer at the Leitz Marseptit 7×50 model, which was produced on the turn of 50’s and 60’s of the twentieth century. Its transmission graph is presented below.
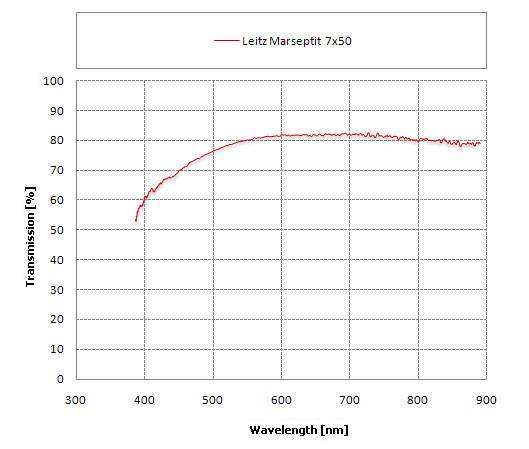 |
When I had an opportunity to look through this pair of binoculars for the first time I was very nicely surprised by the white rendering level. I was used to the performance of single layer coatings, presented by the binoculars from the Eastern Bloc, and I thought I would see the same rendering as in the case of Carl Zeiss Jena instruments. The Leitz fared much better though and it easily understandable why if you consult its transmission graph.
For contemporary standards of the Porro class binoculars the overall transmission doesn’t bowls you over, reaching the maximum level of 81-82%, but it is roughly the same for yellow and red light, for blue getting to about 70%. The difference of 10-15% between yellow-green and blue light doesn’t guarantee a perfect colour rendering but allows to get rid of the strong and unnerving yellowish hue. If you don’t compare the Leitz directly to any contemporary device with an ideal white rendering you can even get an impression that its image is truly clear and white.
The beginning of 70’s of the 20th century meant a revolution of using multilayer coatings, started by the Pentax company. The whole idea is not about putting on one layer of a given thickness but several layers, using different thickness and different materials. What’s more, coatings can be different on different elements so they cooperate the most efficiently within one optical instrument. As an example of good work of multilayer coatings we can show the transmission graph of the Pentax smc DA 40 mm f/2.8 Limited lens.
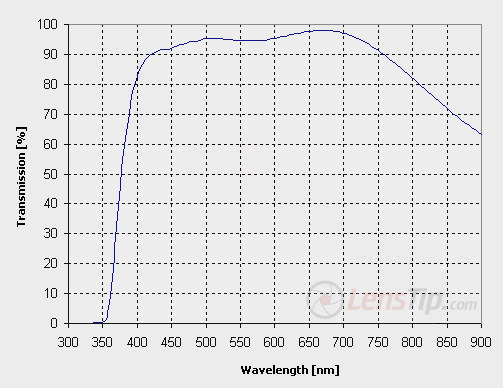
The transmission, reaching 97-98% in the big part of the visible spectrum with 8 surfaces, means on one air-to-glass surface we lose only 0.2-0.3%. As high as the efficiency of coatings produced by the best manufacturers on the market. In the best instruments of the best brands it can even slightly descend below the level of 0.2%.
In the Eastern Bloc multilayer coatings were implemented only in 1978 in Jena. Were they equally good as SMC coatings of Pentax? The transmission graph of the Carl Zeiss Jena Jenoptem 7×50 will allow us to answer that question. The binoculars were produced at the end of the 80s of the twentieth century.
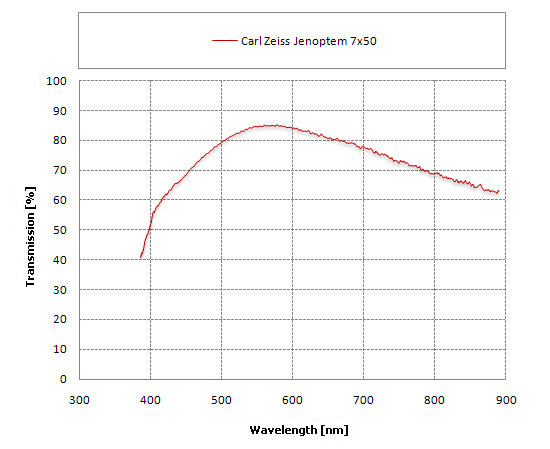 |
As you see the maximum transmission increased because for yellow-green light it reaches now about 85%. It was a bit at the expense of the infrared but such an exchange is a profitable one as our eyes cannot see infrared at all. Compared to single layer coatings from Jena the performance is noticeably better for the blue light as well. The problem of yellowish image wasn’t solved, though. Although the transmission in the centre of visible spectrum increased and the transmission for blue and purple light is higher as well, the difference between them still remains on the level of 20% and it is simply too much to give you a correct colours rendering.
You can also ask here whether or not the Eastern Germany optics can perform any better. The answer is very simple. After the reunification of Germany the factory in Jena couldn’t use Zeiss in its name any longer. It was took over by the Analytik Jena company which, at the very beginning, produced exactly the same binoculars which earlier had been leaving the factory under the name of Docter. The first changes in optics concerned exactly the coatings because those, introduced in German factories in 1978, were considered too weak.
As the time passed also the Docter binoculars have been changed in a more noticeable manner – the optics became a bit more complex and the devices got a solid, rubberized casing. Their construction, though, remained very similar so it’s easy to compare it with that of the Jenoptem 7×50. An immediate comparison is possible when you look at the graph below which presents the transmission of the currently produced Docter Nobilem 7×50 B/GA.
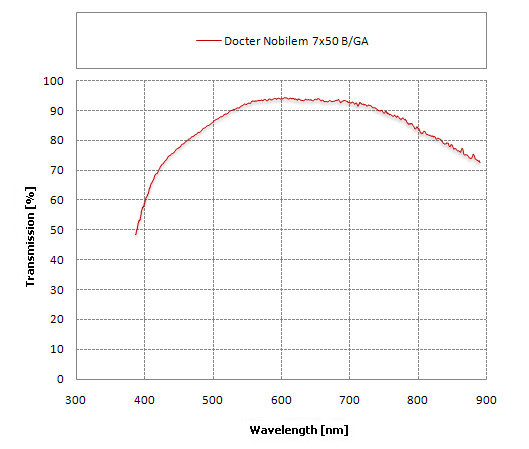 |
Here the situation is much better. The transmission of yellow and green light reaches a very high level of 94%. A distinctly purple hue of the Nobliem’s 7×50 coatings indicates that for these wavelengths the transmission level will be the lowest and it is indeed– for the blue light it gets to 80% and for purple light – about 70%. What’s interesting a definitely better result in this category we got for the Nobilem 8x56 so a bigger brother of the described model. The Docter 7×50 had a noticeably shiny coating on the prisms, indicating that here something must have gone wrong to some extend. As the 8x56 model didn’t feature such a flaw, its transmission was even higher.
As we still want to deal with the Porro 7×50 binoculars we can look for one more example of a contemporary price/quality top of the range product. Steiner is a well-known German producer still manufacturing a lot of Porro binoculars. Below you can admire the transmission graph of the Steiner Commander 7×50 XP.
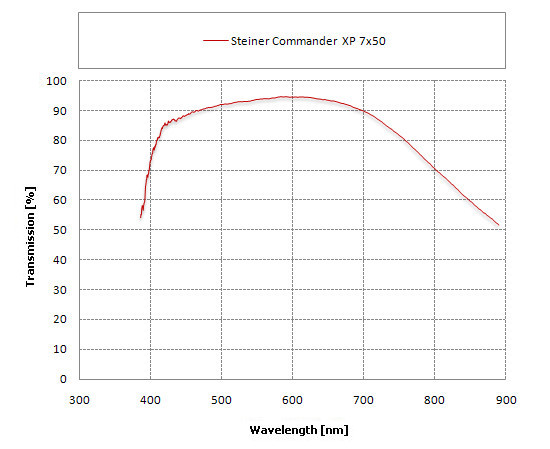 |
The maximum transmission brushes against the level of 95% so, within the margin of error is the same as in the case of the Docter. Overall the Steiner fares better because its visibly superior performance at the sorter wavelengths. In the case of this pair of binoculars even for blue light the transmission reaches a very high level of 90% and for the purple light it is only a few percent lower. The Steiner coatings are of very high quality, not for the first time by the way.
A lot of 7×50 class instruments were featured in this article. To make their number complete and also to post a kind of warning we would like to present one more. In the 50’s and 60’s PZO factories used to produce the PZO LP7×50 model – the predecessor of the LP7×45, described earlier. It happens we also can show the transmission graph of the 7×50 binoculars. It is right below.
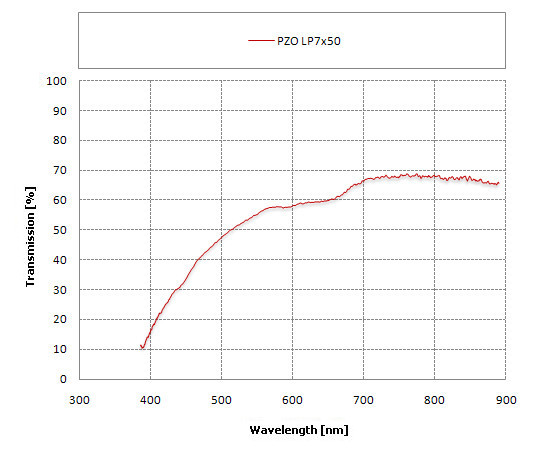 |
It is one of the worse transmission graphs we have had the opportunity to look at. In the centre of the visible spectrum the binoculars don’t let through even 60% of light and the peak of its possibilities is reached on the border of the visible spectrum and infrared. Were the coatings, produced half a century ago in the PZO factories, of so low quality? It turns out that no. The specimen of the LP7×50 model, which fell into our hands, is outside in perfect condition but on closer inspection of its prisms you can see a delicate layer of a substance, most probably mildew. It is a problem quite often met in the case of older optics. If you buy a second-hand instrument on Internet auction sites you, as well as the seller, might not be aware of a noticeable worsening of the optical properties because of unwanted layers, covering the optical elements. The graph above should be considered a warning, then.
Slowly we are wrapping up our article. We want to finish with an optimistic accent. Even more than a dozen years ago multilayer coatings of the highest efficiency were used only in top of the range equipment manufactured by literally few most reputable producers. The situation has been changing lately. A perfect example here is the Korean company Samyang. The transmission graph of the Samyang 85 mm f/1.4 Aspherical IF might be considered a proof of the high quality of antireflection coatings, produced by that company.
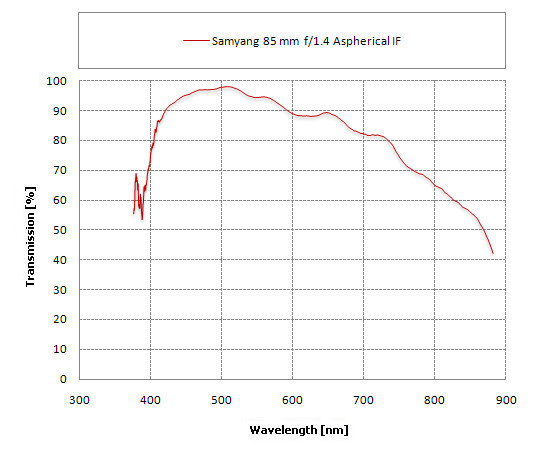 |
I admit I didn’t believe my own eyes when I saw that graph for the first time. First of all the lens performs very well in the blue spectrum. The transmission exceeds 90% already for 420 nm, a very rare occurrence. When we move towards the middle of the visible spectrum the situation becomes even better. Near 500 nm the transmission can reach as high as even 98%! What does it mean? The conclusion is very important because that value means this cheap Korea-manufactured Samyang loses less than 0.2% of light on one air-to-glass surface! Something like space technology under the thatched roofs! Not so long ago such coatings were available only for a big sum of money and now you can get them even in cheap lenses.
The Samyang doesn’t end it. The next example is the Japanese Sigma company. Even 10-15 years ago this company was perceived as a producer of average lenses - their lower prices were often considered their only advantage point. Currently the situation is completely different. Such lenses as the Sigma 50 mm f/1.4 EX DG HSM or the Sigma 85 mm f/1.4 EX DG HSM, launched not so long ago, turn out to be optically better than their equivalents produced by Canon, Nikon, Pentax, or even Zeiss.
Also the opinions, repeated from time to time on different sites, that brand name instruments render colours perfectly whereas such lenses as Sigmas, Tamrons and Tokinas give you a distinctly yellowish image, you can treat as an urban legend. A proof? Here you go.
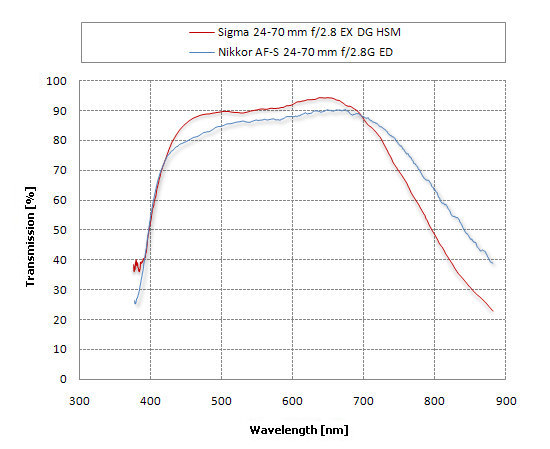 |
The graph below shows the transmission curves of two 24-70 mm f/2.8 lenses produced by Nikon and Sigma. In this pair the Sigma is the more complex one so its task was more difficult. Despite that fact it lets pass through more light for most of the visible spectrum. Both lenses don’t render colours in a perfect way because both curves are slightly slanted, with the highest transmission level in the red part and the lowest in the purple and blue part of the spectrum. However, the slant in both cases is very similar so if the Sigma gives a yellowish hue so does the reputable Nikkor, which is not only less optically complex but also more expensive.
We don’t hesitate to state unambiguously that the new has come - the best optics technologies are no longer available only for the chosen few for a very high amount of money. The number of companies which are able to produce high quality optical instruments has been definitely enlarged lately. As customers we should be very happy at such a turn of events because fiercer competition means lower prices and better customer care.






